卡通渲染PBR效果

​ ​ 上一篇文章简单介绍了卡通渲染的做法。但是用到的光照模型和色阶过渡都比较简单。虽然也能做出一定效果，但是我们总是不希望就此止步不前。所以我接着看其他资料，并把它们总结在这篇文章里。
我们将会使用符合能量守恒的 Lambert公式来计算漫反射项。使用Cook-Torrance模型来计算高光项。基于此计算出PBR的渲染结果。

Cook-Torrance的BRDF

​ ​ Cook-Torrance的BRDF模型公式可以表示如下：

​ ​ 其中左边是漫反射项，右边是高光项。​k_d和​k_s分别代表漫反射强度和镜面反射强度的占比。

Lambert漫反射项

​ ​ 省去推导过程[1]，直接抄公式，可以得到下面的公式

​ ​ 这里​c是反射率，即 albedo，可以把它理解为一束光进入物体表面时，反射的颜色强度。

Cook-Torrance的高光项

​ ​ Cook-Torrance的高光项计算公式引入了一个参数表示粗糙度(_Roughness)。要理解这些公式，推荐先去了解微表面模型，在我的这篇文章[2]中有介绍。

​ ​ 其中​D是法线分布函数，是一个浮点数，它表示的是微表面中与半程向量一致的法线百分比，是一个根据粗糙度计算的评估结果，一般我们都只说法线分布，却不提半程向量，然后直接进入公式，容易引发读者理解断层，我在这强调一下。
​ ​ ​F是菲涅尔项，它表示的是反射和折射的比例，越接近边缘的反射比例越高。
​ ​ ​G是遮蔽系数，它微表面上的遮挡系数，也是一个评估值，一般我们也把它称为几何分布函数，也容易误解，它也是一个评估值，表示有多少百分比的微表面不会被遮挡。这类函数通常需要同时评估观察方向的遮蔽系数和入射方向的遮蔽系数。

​ ​ 剩下的就直接抄公式

法线分布函数

​ ​ 法线分布函数其实不是一个，只要符合能量守恒定律，按一定统计理论提出的计算模型都可以作为法线分布函数。这里给出我们使用 Trowbridge-Reitz GGX公式来计算法线分布。公式如下：

​ ​ 在这里​h表示用来与平面上微平面做比较用的半程向量，而​\alpha表示表面粗糙度。直接抄公式也很简单。

float TrowbridgeReitzGGX(float3 normal, float3 halfVec, float alpha)
{
    float alpha2 = alpha * alpha;
    float ndh = max(dot(normal, halfVec),0.0f);
    float ndh2 = ndh * ndh;
    float temp = (ndh2)*(alpha2-1) + 1;
    return alpha2/(PI*temp*temp);
}

几何分布函数

​ ​ 我们将要使用的几何函数是GGX与 Schlick-Beckmann近似的结合体，因此又称为 Schlick-GGX。

​ ​ 其中​k是与​\alpha相关的值，它取决于我们计算的光照类型。这里我们计算的是直接光，计算公式如下：

​ ​ ​v是观察方向，它可以是摄像机的方向，也可以是光方向。我们使用 Smith方法来把两个方向都考虑进去。

float SchlickGGX(float ndv, float k)
{
    float denom = ndv*(1.0f - k) + k;
    return ndv/denom;
}

float GeometrySmith(float3 normal, float3 viewDir, float3 lightDir, float k)
{
    float NdotV = max(dot(normal, viewDir), 0.0);
    float NdotL = max(dot(normal, lightDir), 0.0);
    float ggx1 = SchlickGGX(NdotV, k);
    float ggx2 = SchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

菲涅尔方程

​ ​ 菲涅尔方程描述的是物体表面反射光线的比例，该比例随着观察角度而变化。通常，直视表面时反射比例越少，而视线与表面越平齐则反射光线越多。例如观察水面时，直视时更容易看到水底，因为该观察角度反射光线少，折射光线多。当视线与水面平齐，折射光线少，反射光线多，所以可以看到远处物体在水面的倒影。

​ ​ 下面的 Fresnel-Schlick公式可以近似描述该现象。

​ ​ 其中，​F_0是基础反射率，可以认为是物体表面的颜色。

float3 FresnelSchlick(float3 normal, float3 viewDir, float3 baseFresnel, float fresnelPower)
{
    float cosTheta = max(dot(normal, viewDir), 0);
    return baseFresnel + (1.0f - baseFresnel)*pow(1.0f - cosTheta, fresnelPower);
}

菲涅尔反射与金属工作流

​ ​ 对于大部分电介质（非金属）表面材质，菲涅尔方程是正确的。对于导体（金属）表面，并不总是正确。可是又希望能够用上面的公式来进行近似计算，科学家们通过测量导体表面的基础反射率。测量的结果是直视表面时，导体（金属）表面的基础反射率，也可以认为是表面颜色。

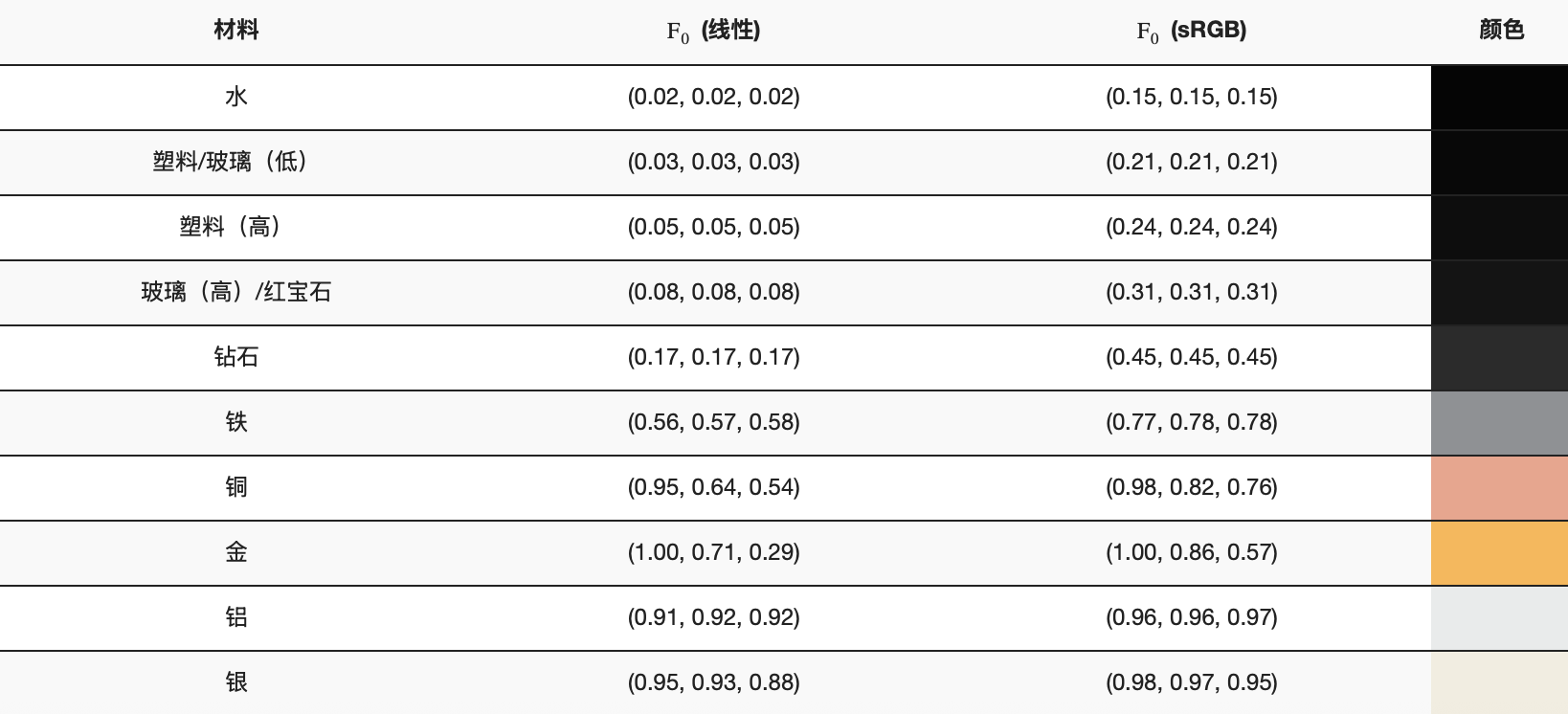
​ ​ 然后，我们可以定义一个金属度（_Matallic）的参数，值的范围是0-1，然后用测量的表面反射率​F_0与物体表面颜色进行插值。金属度为0时取表面颜色​albedo，金属度为为1时去​F_0，这样两种类型的表面就可以统一使用该公式了。

float3 FresnelSchlick(float3 normal, float3 viewDir, float3 baseFresnel, float fresnelPower)
{
    float cosTheta = max(dot(normal, viewDir), 0);
    return baseFresnel + (1.0f - baseFresnel)*pow(1.0f - cosTheta, fresnelPower);
}
...
float3 fresnelAmount = _FresnelAmount;
fresnelAmount = lerp(albedo, fresnelAmount, _Metallic);
float3 fresnel = FresnelSchlick(normal,viewDirWS, fresnelAmount,_FresnelPower);

​ ​ 这样，我们就定义了基于金属工作流的PBR模型。

​k_d和​k_s的计算

​ ​ 在 Cook-Torrance模型中，​k_s表示的是反射系数，该值可以直接用 Fresnel来表示，​k_d的计算要考虑金属度，如果是金属表面，不会有漫反射光，而非金属表面才会散射光线。所以最终的计算如下：

float3 ks = fresnel;
float3 kd = 1.0f - ks;
kd *= (1.0f - _Metallic);

最终代码

#ifndef TOON_PBR_FORWARD_PASS
#define TOON_PBR_FORWARD_PASS

#include "ToonPBRInput.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl"

struct VSInput
{
    float4 positionOS   : POSITION;
    float3 normalOS     : NORMAL;
    float4 tangentOS    : TANGENT;
    float2 uv           : TEXCOORD0;
};

struct PSInput
{
    float4 positionCS:SV_POSITION;
    float2 uv:TEXCOORD0;
    float3 normalWS:TEXCOORD1;
    float3 positionWS:TEXCOORD2;
    float3 viewDirWS:TEXCOORD3;
#ifdef _ENABLEBUMPMAP_ON
    float4 tangentToWorld0: TEXCOORD4;
    float4 tangentToWorld1: TEXCOORD5;
    float4 tangentToWorld2: TEXCOORD6;
#endif
};

PSInput ToonVert(VSInput vertex)
{
    PSInput output;
      
    output.positionCS = TransformObjectToHClip(vertex.positionOS);

    VertexNormalInputs normalInput = GetVertexNormalInputs(vertex.normalOS, vertex.tangentOS);
   
  
    output.normalWS = normalInput.normalWS;
    output.positionWS = TransformObjectToWorld(vertex.positionOS).xyz;
    output.viewDirWS = GetWorldSpaceViewDir(output.positionWS);
    output.uv = vertex.uv;
  
#ifdef _ENABLEBUMPMAP_ON
    float3 worldTangent = normalInput.tangentWS;
    float3 worldNormal = normalInput.normalWS;
    float3 worldBitangent = normalInput.bitangentWS;

    output.tangentToWorld0 = float4(worldTangent.x, worldBitangent.x, worldNormal.x, output.positionWS.x);
    output.tangentToWorld1 = float4(worldTangent.y, worldBitangent.y, worldNormal.y, output.positionWS.y);
    output.tangentToWorld2 = float4(worldTangent.z, worldBitangent.z, worldNormal.z, output.positionWS.z);
#endif

    return output;
}


float TrowbridgeReitzGGX(float3 normal, float3 halfVec, float alpha)
{
    float alpha2 = alpha * alpha;
    float ndh = max(dot(normal, halfVec),0.0f);
    float ndh2 = ndh * ndh;
    float temp = (ndh2)*(alpha2-1) + 1;
    return alpha2/(PI*temp*temp + 0.00001f);
}

float SchlickGGX(float ndv, float k)
{
    float denom = ndv*(1.0f - k) + k + 0.00001f;
    return ndv/denom;
}

float GeometrySmith(float3 normal, float3 viewDir, float3 lightDir, float roughness)
{
    float r = (roughness +1);
    float k = (r*r)/8.0f;
  
    float NdotV = max(dot(normal, viewDir), 0.0);
    float NdotL = max(dot(normal, lightDir), 0.0);
    float ggx1 = SchlickGGX(NdotV, k);
    float ggx2 = SchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

float3 FresnelSchlick(float3 normal, float3 viewDir, float3 baseFresnel, float fresnelPower)
{
    float cosTheta = max(dot(normal, viewDir), 0);
    return baseFresnel + (1.0f - baseFresnel)*pow(1.0f - cosTheta, fresnelPower);
}

float4 ToonFragment(PSInput input):SV_TARGET
{
    float3 ambient = _GlossyEnvironmentColor.rgb;
  
    Light mainLight = GetMainLight();
    float3 lightDir = normalize(mainLight.direction);

	float4 albedo = SAMPLE_TEXTURE2D(_BaseMap, sampler_BaseMap, input.uv);
  
	float3 normal = NormalizeNormalPerPixel(input.normalWS);

	float3 viewDirWS = normalize(input.viewDirWS);

    float3 halfVec = normalize(viewDirWS + lightDir);

    //  Cook-Torrance brdf
    float NDF = TrowbridgeReitzGGX(normal, halfVec, _Roughness);
    float G = GeometrySmith(normal, viewDirWS, lightDir, _Roughness);
  
    float3 fresnelAmount = _FresnelAmount;
    fresnelAmount = lerp(fresnelAmount,albedo.rgb, _Metallic);
	float3 fresnel = FresnelSchlick(normal, halfVec, fresnelAmount, _FresnelPower);

    float ndl = max(dot(lightDir, normal), 0.0f);
    float ndv = max(dot(normal, viewDirWS),0.0f);
  
	float3 cookTorrance = (NDF * G * fresnel) / (4 * (ndl) * (ndv) + 0.0001f);

    float3 ks = fresnel;
    float3 kd = 1.0f - ks;
    kd *= (1.0f - _Metallic);

	float3 diffuse = albedo.rgb / PI;

	float3 color = _BaseColor.rgb * (kd * diffuse + ks * cookTorrance) * mainLight.color*ndl + albedo.rgb*ambient;

	return float4(color, 1);
}
#endif

​ ​ 使用上面的代码来渲染时，物体表面的光泽总是会偏暗。这可能是使用的 albedo贴图并不是特别好，并且需要配合法线贴图等其他贴图才能获得比较好的效果。比如我自己使用的模型和贴图，就会获得偏暗的结果。如果不除以​\pi，可以得到比较好的结果（手臂和身体部分）

Cook-Toorance模型的卡通化改进

​ ​ 要将渲染结果卡通化，主要把漫反射的明暗和高光的明暗进行二值化处理。所以这部分内容，我会从漫反射的处理和高光部分的处理上着手。最后把我们之前的边缘光抄过来。

漫反射

​ ​ 这里要介绍漫反射的明暗二值化，主要是通过 smoothstep来完成。关于该函数前面已有介绍，这里想把色阶分为三段，可以把 smoothstep函数进行加权求和来达到在多个区间内平滑过渡和极化的操作。

​ ​ 如果要构造三色阶，可以通过 smoothstep构造出下面的函数，图像如下:

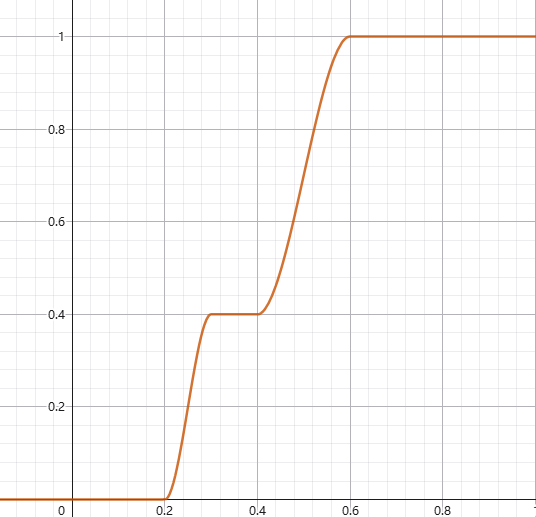
​ ​ 应用到Shader中，可以得到下面的明暗分布图：

float ndl = max(dot(lightDir, normal), 0.0f);

float rampIntensity = smoothstep(_RampThresholdHigh - 0.5f * _RampThresholdSmoothHigh, _RampThresholdHigh + 0.5f *
		_RampThresholdSmoothHigh, ndl) * (1 - _RampIntensityMid)
    + smoothstep(_RampThresholdLow - 0.5f * _RampThresholdSmoothLow, _RampThresholdLow + 0.5f * _RampThresholdSmoothLow, ndl)*
    _RampIntensityMid;

​ ​ 这里用两个 smooth参数来控制边界的锐利程度，我们可以用粗糙度(_Roughness)来映射它。

float ndl = max(dot(lightDir, normal), 0.0f);

float rampSmooth = _RampThresholdSmoothScale * pow(_RampThresholdSmoothBase, _Roughness);

float rampIntensity = smoothstep(_RampThresholdHigh - 0.5f * rampSmooth, _RampThresholdHigh + 0.5f * rampSmooth, ndl) * (1 - _RampIntensityMid) + smoothstep(_RampThresholdLow - 0.5f * rampSmooth, _RampThresholdLow + 0.5f * rampSmooth, ndl) * _RampIntensityMid;

​ ​ 这样，就可以通过几个参数来控制过渡边界的锐利程度。

高光项

​ ​ 在 Cook-Torrance的高光计算中，几何分布函数决定了会被光照亮的部分。主要是对法线分布函数的调整。根据MEng Zheng他的博文里给出的公式[3]，我们可以计算一个法线分布评估的最大值，然后定义一个百分比来控制分割阈值，大于该值时会二值化为1，小于该值时会二值化为0。为了符合物理直觉，将该计算结果与粗糙度关联，越平滑的物体表面，它的高光面积越集中，亮度越高，越粗糙的表面，高光面积越大，亮度越低。

float NDF0 = TrowbridgeReitzGGX(1, _Roughness);
float NDFBounds = NDF0 * _GGXBoundsScale;
float NDF = TrowbridgeReitzGGX(normal, halfVec, _Roughness);

float specularSmooth = _SpecularRampSmoothScale * pow(_SpecularRampSmoothBase, _Roughness);

NDF = smoothstep(NDFBounds - specularSmooth * 0.5f, NDFBounds + specularSmooth * 0.5F, NDF);

NDF = NDF * pow(_SpecularAttenuationBase, 1 - _Roughness);

边缘光

​ ​ 我们把之前的边缘光代码移植过来。并改成使用 Freshnel-Schlick来计算，并进行二值化。

float3 rimAmount = float3(_RimAmount, _RimAmount, _RimAmount);
float3 fresnel = FresnelSchlick(normal, viewDirWS, rimAmount, _FresnelPower);
fresnel *= ndl;
float rimSize = 1 - _RimAmount;
float3 rimSmooth = smoothstep(rimSize, rimSize * 1.1f, fresnel) * _RimIntensity;

最终代码

#ifndef TOON_PBR_FORWARD_PASS
#define TOON_PBR_FORWARD_PASS

#include "ToonPBRInput.hlsl"
#include "Packages/com.unity.render-pipelines.universal/ShaderLibrary/Lighting.hlsl"

struct VSInput
{
    float4 positionOS   : POSITION;
    float3 normalOS     : NORMAL;
    float4 tangentOS    : TANGENT;
    float2 uv           : TEXCOORD0;
};

struct PSInput
{
    float4 positionCS:SV_POSITION;
    float2 uv:TEXCOORD0;
    float3 normalWS:TEXCOORD1;
    float3 positionWS:TEXCOORD2;
    float3 viewDirWS:TEXCOORD3;
#ifdef _ENABLEBUMPMAP_ON
    float4 tangentToWorld0: TEXCOORD4;
    float4 tangentToWorld1: TEXCOORD5;
    float4 tangentToWorld2: TEXCOORD6;
#endif
};

PSInput ToonVert(VSInput vertex)
{
    PSInput output;
      
    output.positionCS = TransformObjectToHClip(vertex.positionOS);

    VertexNormalInputs normalInput = GetVertexNormalInputs(vertex.normalOS, vertex.tangentOS);
   
  
    output.normalWS = normalInput.normalWS;
    output.positionWS = TransformObjectToWorld(vertex.positionOS).xyz;
    output.viewDirWS = GetWorldSpaceViewDir(output.positionWS);
    output.uv = vertex.uv;
  
#ifdef _ENABLEBUMPMAP_ON
    float3 worldTangent = normalInput.tangentWS;
    float3 worldNormal = normalInput.normalWS;
    float3 worldBitangent = normalInput.bitangentWS;

    output.tangentToWorld0 = float4(worldTangent.x, worldBitangent.x, worldNormal.x, output.positionWS.x);
    output.tangentToWorld1 = float4(worldTangent.y, worldBitangent.y, worldNormal.y, output.positionWS.y);
    output.tangentToWorld2 = float4(worldTangent.z, worldBitangent.z, worldNormal.z, output.positionWS.z);
#endif

    return output;
}


float TrowbridgeReitzGGX(float3 normal, float3 halfVec, float alpha)
{
    float alpha2 = alpha * alpha;
    float ndh = max(dot(normal, halfVec),0.0f);
    float ndh2 = ndh * ndh;
    float temp = (ndh2)*(alpha2-1) + 1;
    return alpha2/(PI*temp*temp + 0.00001f);
}

float TrowbridgeReitzGGX(float ndh, float alpha)
{
	float alpha2 = alpha * alpha;
	float ndh2 = ndh * ndh;
	float temp = (ndh2) * (alpha2 - 1) + 1;
	return alpha2 / (PI * temp * temp + 0.00001f);
}

float SchlickGGX(float ndv, float k)
{
    float denom = ndv*(1.0f - k) + k + 0.00001f;
    return ndv/denom;
}

float GeometrySmith(float3 normal, float3 viewDir, float3 lightDir, float roughness)
{
    float r = (roughness +1);
    float k = (r*r)/8.0f;
  
    float NdotV = max(dot(normal, viewDir), 0.0);
    float NdotL = max(dot(normal, lightDir), 0.0);
    float ggx1 = SchlickGGX(NdotV, k);
    float ggx2 = SchlickGGX(NdotL, k);

    return ggx1 * ggx2;
}

float3 FresnelSchlick(float3 normal, float3 viewDir, float3 baseFresnel, float fresnelPower)
{
    float cosTheta = max(dot(normal, viewDir), 0);
    return baseFresnel + (1.0f - baseFresnel)*pow(1.0f - cosTheta, fresnelPower);
}

float4 ToonFragment(PSInput input):SV_TARGET
{
    float3 ambient = _GlossyEnvironmentColor.rgb;
  
    Light mainLight = GetMainLight();
    float3 lightDir = normalize(mainLight.direction);

	float4 albedo = SAMPLE_TEXTURE2D(_BaseMap, sampler_BaseMap, input.uv);

  
    #ifdef _ENABLEBUMPMAP_ON
    float3 normal = normalize(UnpackNormalScale(SAMPLE_TEXTURE2D(_BumpMap, sampler_BumpMap, input.uv), _BumpScale));
    normal = normalize(float3(dot(normal, input.tangentToWorld0), dot(normal, input.tangentToWorld1), dot(normal, input.tangentToWorld2)));
    #else
	float3 normal = NormalizeNormalPerPixel(input.normalWS);
    #endif

	float ndl = max(dot(lightDir, normal), 0.0f);

	float rampSmooth = _RampThresholdSmoothScale * pow(_RampThresholdSmoothBase, _Roughness);

	float rampIntensity = smoothstep(_RampThresholdHigh - 0.5f * rampSmooth, _RampThresholdHigh + 0.5f * rampSmooth, ndl) * (1 - _RampIntensityMid)
						  + smoothstep(_RampThresholdLow - 0.5f * rampSmooth, _RampThresholdLow + 0.5f * rampSmooth, ndl) * _RampIntensityMid;

	float3 diffuse = rampIntensity * albedo.rgb*_BaseColor;

	float3 viewDirWS = normalize(input.viewDirWS);

    float3 halfVec = normalize(viewDirWS + lightDir);

    //  Cook-Torrance brdf
	float NDF0 = TrowbridgeReitzGGX(1, _Roughness);
	float NDFBounds = NDF0 * _GGXBoundsScale;
    float NDF = TrowbridgeReitzGGX(normal, halfVec, _Roughness);

	float specularSmooth = _SpecularRampSmoothScale * pow(_SpecularRampSmoothBase, _Roughness);

	NDF = smoothstep(NDFBounds - specularSmooth * 0.5f, NDFBounds + specularSmooth * 0.5F, NDF);

	NDF = NDF * pow(_SpecularAttenuationBase, 1 - _Roughness);

	float G = GeometrySmith(normal, viewDirWS, lightDir, _Roughness);

	float ndv = max(dot(normal, viewDirWS), 0.0f);


	float cookTorrance = (NDF * G) / (4 * (ndl) * (ndv) + 0.0001f);

	float3 specular = float3(cookTorrance, cookTorrance, cookTorrance);

	float3 rimAmount = float3(_RimAmount, _RimAmount, _RimAmount);
	float3 fresnel = FresnelSchlick(normal, viewDirWS, rimAmount, _FresnelPower);
	fresnel *= ndl;
	float rimSize = 1 - _RimAmount;
	float3 rimSmooth = smoothstep(rimSize, rimSize * 1.1f, fresnel) * _RimIntensity;

	float3 radiance = mainLight.color;

	return float4((diffuse + specular + rimSmooth) * radiance + albedo.rgb * ambient, 1);
}
#endif

次表面散射

​ ​ 经过上面的着色，可以渲染出还满意的效果。但是仍差点意思。对于人体的皮肤，在背光面会有一些红色的透光。

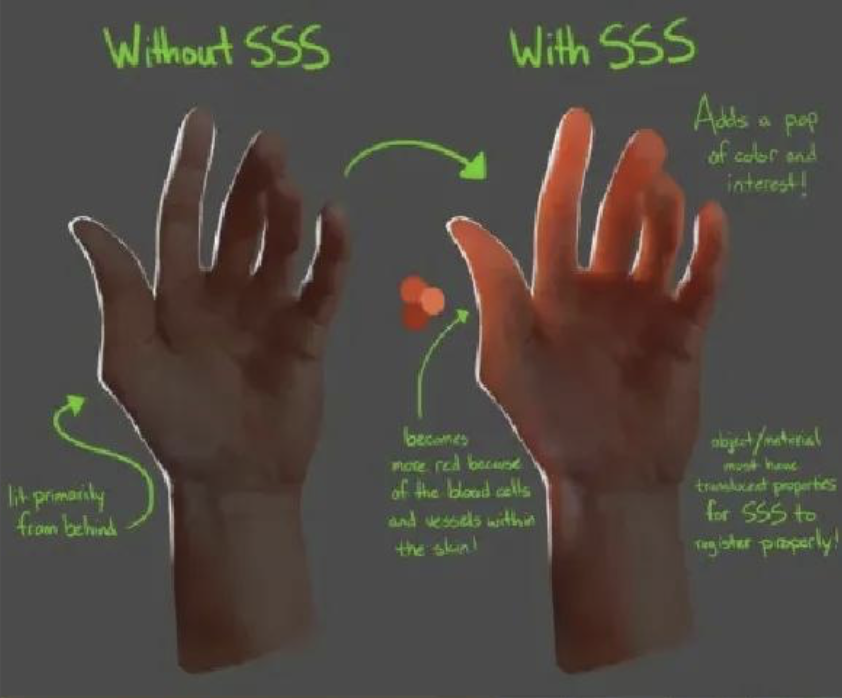
​ ​ 这是因为皮肤介质是分为多层的。当光射入皮肤表面时，在皮肤的表面会发生散射，这是BRDF部分。而有一部分光会从入射点进入介质内，再从其他出射点出来，有的方向会进入人眼睛，这就是我们在背光时，可以看到皮肤会变得通透的原因。

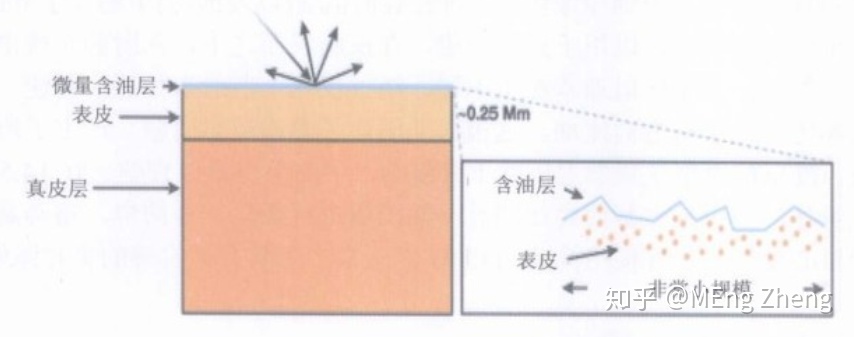
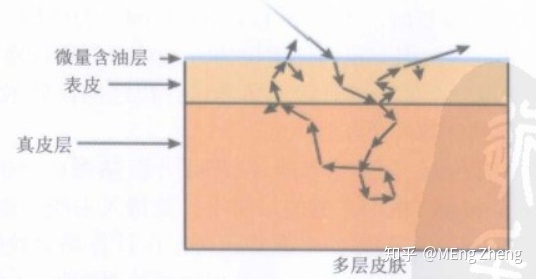
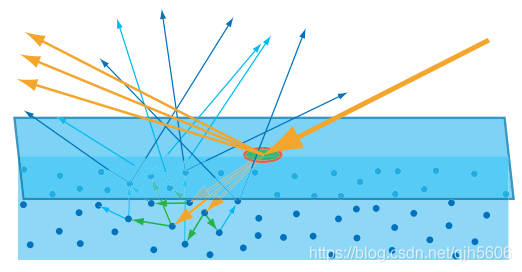
​ ​ 这样的材质有很多，牛奶，蜡烛，玉石都是可以这些可以透光的材质。

​ ​ 为了实现这类效果。业界提出了许多的方法，包括：

• 纹理空间次表面散射
• 屏幕空间的次表面散射
• 预积分次表面散射

​ ​ 每种方法都有自己的理论和说法。但不一定符合物理，本着效果看起来合理，便是正确的原则，这里就不深究是否符合物理规律了。我们这里主要介绍预积分的次表面散射。

预积分的次表面散射

​ ​ 预积分的次表面散射技术基于两个观察结论：肉眼可见的次表面散射现象只会出现在表面曲率较大且正处于明暗交界线位置的区域。换而言之，次表面散射现象的强弱只和两个量有关，一是表面的曲率，而是法线和光线的点积。表面曲率越大，次表面散射在纹理空间的扩散范围就越大。

​ ​ 预积的次表面散射有一个假设前提，即：表面上的每个点，都会受到来自表面其他点的散射影响。

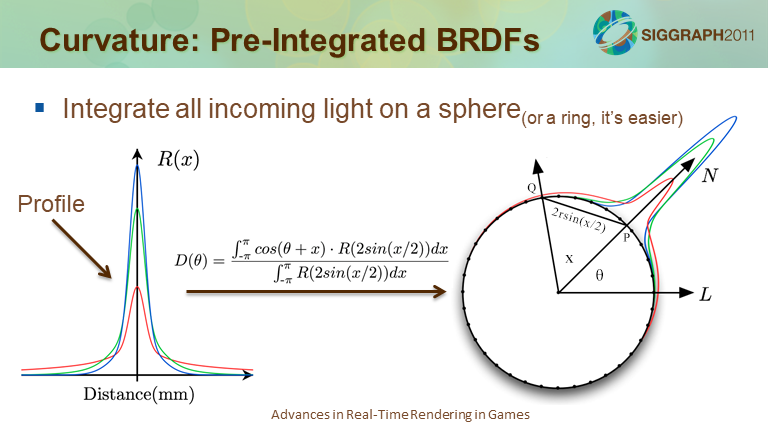
​ ​ 公式如上图。假设表面上的一个点​P，发线方向为​N，光方向为​L，​N与​L的夹角为​\theta。该点会受到另一个点的散射影响，假设该点法线方向是​N_x散射。该点接收到的光能是​N_x \cdot L，换算一下，就等于​cos(\theta+x)。那么​P点受到圆环上其他点的能量就是一个积分式。

​ ​ 假设散射系数是​R(d)，它是一个与距离关的函数，该距离指的是出射点和入射点的直线距离，则

​ ​ 这里​cos(\theta + x)的范围是​[-1,1]，对于背光面的点，可以不用考虑，所以可以把公式改成下面的形式

​ ​ 接下来是散射系数​R(d)。它是一个与距离有关的函数。在圆环积分中，这里距离​d=2rsin(\frac{\theta}{2})（上面PPT中的图）。所以公式可以改写成下面的形式:

​ ​ 我们的目标是要找到一个满足皮肤次表面特性的函数，并且要做到能量守恒，那么需要它在圆环积分上的值为1。所以需要列方程求解一个常数​k，可列方程如下：

​ ​ 经过推导，可得

​ ​ 所以最终的公式为：

​ ​ 然后是R的定义。这里R是一系列高斯函数的加权和，距离​d作为均值，​v是方差

​ ​ 对于皮肤而言，英伟达算出了方差和RGB的权值，用5个高斯函数去表示。

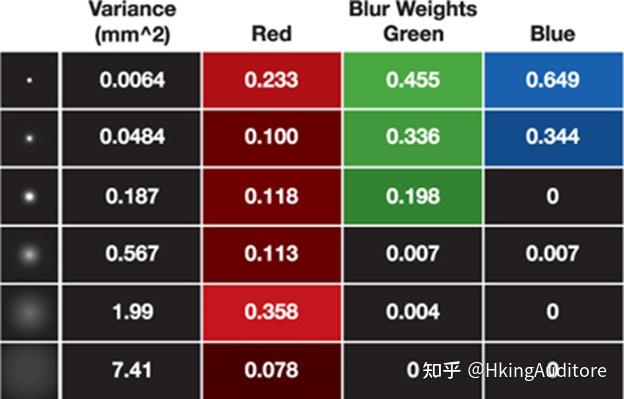
​ ​ 转换成代码就是下面的形式：

float Gaussian(float v, float r)
{
    return 1.0 / sqrt(2.0 * PI * v) * exp(-(r * r) / (2 * v));
}

float3 Scatter(float r)
{
	// coefficients from gpu gems 3 - advance skin rendering
	return Gaussian(0.0064 * 1.1414, r) * float3(0.233, 0.455, 0.649) +
		Gaussian(0.0484 * 1.1414, r) * float3(0.100, 0.336, 0.334) +
		Gaussian(0.1870 * 1.1414, r) * float3(0.118, 0.198, 0.000) +
		Gaussian(0.5670 * 1.1414, r) * float3(0.113, 0.007, 0.007) +
		Gaussian(1.9900 * 1.1414, r) * float3(0.358, 0.004, 0.000) +
		Gaussian(7.4100 * 1.1414, r) * float3(0.078, 0.000, 0.000);
}

​ ​ 下面就是计算预积分的代码：

// Each #kernel tells which function to compile; you can have many kernels
#pragma kernel CSMain

const static float PI = 3.1415926535897932f;

float Gaussian(float v, float r)
{
    return 1.0 / sqrt(2.0 * PI * v) * exp(-(r * r) / (2 * v));
}

float3 Scatter(float r)
{
	// coefficients from gpu gems 3 - advance skin rendering
	return Gaussian(0.0064 * 1.1414, r) * float3(0.233, 0.455, 0.649) +
		Gaussian(0.0484 * 1.1414, r) * float3(0.100, 0.336, 0.334) +
		Gaussian(0.1870 * 1.1414, r) * float3(0.118, 0.198, 0.000) +
		Gaussian(0.5670 * 1.1414, r) * float3(0.113, 0.007, 0.007) +
		Gaussian(1.9900 * 1.1414, r) * float3(0.358, 0.004, 0.000) +
		Gaussian(7.4100 * 1.1414, r) * float3(0.078, 0.000, 0.000);
}

float3 IntergrateDiffuseScatteringOnRing(float cosTheta, float Radius)
{
	// Angle from lighting direction
	float theta = acos(cosTheta);
	float3 totalWeights = 0;
	float3 totalLight = 0;
	float inc = 0.0001;

	// fix the Integration domain base base on https://zhuanlan.zhihu.com/p/384541607
	for (float a = -PI/2 ; a <= PI/2 ; a += inc)
	{
		float sampleAngle = theta + a;
		float diffuse = saturate(cos(sampleAngle));
		float sampleDist = abs(2.0 * Radius * sin(a * 0.5));
		float3 weights = Scatter(sampleDist);
		totalWeights += weights;
		totalLight += diffuse * weights;
	}
	return totalLight / max(totalWeights, 0.0001);
}

// Create a RenderTexture with enableRandomWrite flag and set it
// with cs.SetTexture
RWTexture2D<float4> Result;

float RTWidth;
float RTHeight;

[numthreads(32,32,1)]
void CSMain (uint3 id : SV_DispatchThreadID)
{
    // TODO: insert actual code here!
    float4 colorOut = (0, 0, 0, 1);
  
	float ndl = (id.x / RTWidth)*2.0f-1.0f;
    float ratioY = id.y/RTHeight;
    float radius = 1.0f / (ratioY + 0.0001f);
  
    colorOut.rgb = IntergrateDiffuseScatteringOnRing(ndl, radius).rgb;
  
    Result[id.xy] = colorOut;
}

预积分贴图的使用

​ ​ 完成预积分之后，LUT贴图的使用就很简单，横轴是漫反射​n\cdot L的结果。纵轴是曲率。

​ ​ 因为在生成LUT图时，竖直方向上我们是以理想小球半径的倒数，即用 来排布的，在采样时，我们就应当反求出每个像素点对应的小球半径。

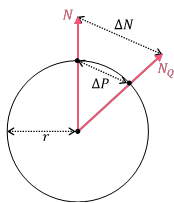
​ ​ 这里用相似三角形，即可求出

​ ​ 即可求出该点的曲率。这样我们就可以采样LUT贴图，获得次表面散射的结果。在此基础上，定义一下常量来控制，得到看起来不错的效果：

....
final = (diffuse + specular + rimSmooth) * radiance + albedo.rgb * ambient;
....
float deltaWorldNormal = length(fwidth(normal));
float deltaWorldPos = length(fwidth(input.positionWS)) + 0.000001f;
float curvature = saturate((deltaWorldNormal / deltaWorldPos)) * _CurveFactor;
float t = (1.0-_Thickness) * saturate(dot(-normal,lightDir));
float NoL = saturate(ndl * 0.5f + 0.5f);
float2 LutTex = float2(NoL, curvature);
float3 subSurface = SAMPLE_TEXTURE2D(_SSSLUT, sampler_SSSLUT, LutTex).rgb*t;
final += subSurface*_SSSWeight*_SSSColor.rgb;

（这个模型不太好，所以背部有一个亮三角，这里的法线可能有问题）

参考资料

[1] 基于物理的渲染：微平面理论(Cook-Torrance BRDF推导) - 知乎

[2] PBR基础总结 - 寒江雪 (Venterwu)

[3] 卡通渲染基本光照模型的实现 - 知乎

[4] 图形学基础：深度解析皮肤渲染的次表面散射与预积分技术

[5] 从零开始的预积分次表面散射