稀疏八叉树的编码总结
八叉树是用于三维场景空间划分经典的数据结构。相对地,二维空间可以用四叉树表示,它们只有维度上的区别,性质基本相似。因此,我们这里就只以八叉树为例子进行说明,四叉树就留给大家自己"举一反三"。
本文主要介绍如下的内容:
- 八叉树与稀疏八叉树
- 稀疏八叉树的编码
- 大范围场景的划分
- 稀疏八叉树与三维空间寻路
其中,对于稀疏八叉树的编码,我将介绍两种表示方法。一种是网上能看到的Morton Code,另一种是我基于Morton编码的改进, 由于没有找到出处,我把它称为VTCode。
八叉树与稀疏八叉树
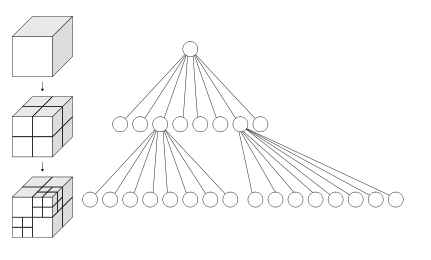
多叉树形结构很好理解。就是树上每个节点都有N个子节点,八叉树就是8个子节点。每一个节点都表示一个空间范围,用AABB包围盒表示,也可以叫做体素(Voxel)。如下图所示可以表示一个八叉树的节点及其子节点。
八叉树的根节点表示一个空间范围。在进行分裂时,将输入的多边形网格数据递归地与子节点进行相交,分裂,直到最低的一层为止。这里最低一层的深度,是由业务需求决定的。理论上它可以分得非常精细,当然会增加内存的开销和递归查询时的时间消耗,在使用的时候,就要根据需求进行取舍,主要还是内存开销较大。根据实践经验,4000m x 4000m x 4000m 的场景,在Unity上构建时就已经崩溃,最大深度我已经不记得了,不过这不重要,我们后续介绍的内容就是为了解决这个问题的。
稀疏八叉树与八叉树不同的一点在于,八叉树是完全分裂的,而稀疏八叉树不是。当八叉树的一个节点需要分出子节点时,它的八个子节点都要划分出来,哪怕它里面什么内容都没有。而稀疏八叉树的节点在分裂时,只有当子节点和输入的几何体相交时,才会生成子节点。这样做有一个好处,即稀疏八叉树的节点,都是有内容的,而不在树上的节点,都是没有内容的。这样使用稀疏八叉树对场景进行划分,会比完全划分的八叉树使用的内存更少。
稀疏八叉树的编码
经过前面的介绍,大家应该能够对八叉树和稀疏八叉树有一个清晰的认知了。下面介绍的内容,就是如何使用字典来表示树结构,以实现快速的插入和查询。
所谓字典存树,就是将稀疏八叉树上的节点,都通过编码进行表示,然后作为字典的Key值,映射一个byte数据。这个byte有8比特,它就可以用来表示当前节点的第i个子节点是否是阻塞节点,1表示是阻塞节点,0表示不是。所谓阻塞节点,就是“被物体填满的节点”。这类节点通常是稀疏八叉树的叶子节点,当一个稀疏节点的8个节点都是阻塞节点时,那么这个稀疏节点变成了阻塞节点。并递归地向父亲节点逐层标记。
那么这就引入了节点类型的概念。在稀疏八叉树中,只有三类节点类型,分别是:
- 稀疏节点
- 阻塞节点
- 空节点
这三类节点有如下特点:
- 稀疏节点:有子节点,但子节点是阻塞节点或空节点
- 阻塞节点:已经被划分出来的节点,子节点全是阻塞节点,自身也是阻塞节点。叶子节点是最小的阻塞节点
- 空节点:没有被划分出来的节点。
这三类节点,并不是都需要存到字典里的。只有稀疏节点会存在字典中。所以在字典中,就只有稀疏节点的编码。在计算出一个节点编码时,如果该编码在字典中,则是稀疏节点,如果该节点不在字典中,它就可能是空节点或阻塞节点。这就需要向上回溯,找到该编码所属的稀疏节点,计算出该节点处在稀疏节点的子空间索引(即前面提到的第i个子节点),然后根据该稀疏节点映射的byte数据,判断出该节点是阻塞节点还是空节点。如果byte数据中,对应的比特位为0,则是空节点,为1则是阻塞节点。

这就引入我接下来要介绍的稀疏八叉树编码。基于网上的公开资料,我只了解到了Morton Code编码系统,基于Morton Code,我对它进行了改进,使得编码效率更快,且容易理解。在后面的内容,我会逐步介绍这两套编码原理。
莫顿码(Morton Code)
这里介绍莫顿码,用的是32 bits整数来说明,理论上有无限的比特,编码的长度可以一直扩展。对于32 bits的莫顿编码,要编码三维空间的三个坐标(X,Y,Z),每个坐标平均需要使用10个比特,有2个比特是用不到的。不过为了充分利用空间,我们用1个比特来表示节点在稀疏八叉树上的深度。接下来,我将会从单个坐标开始,介绍对一个坐标的编码处理,然后介绍三个坐标编码的合成,最后介绍节点所在层数的表示方法。这样就能很好地表示稀疏八叉树上的节点了。接着会介绍父子节点之间的编码关系,最后说明编码背后,每一个比特所代表的含义。
单一整数编码
莫顿编码是需要考虑维度的。在有限的比特位内(我们这里是32 bits),把每一个维度的坐标都合到一起。以三维坐标(X,Y,Z)为例,这里每个坐标都是整数,占10个比特。为了把他们合并到一起,莫顿编码定义,每个坐标都需要在每个比特位之间,插入两个0。如下图所示。
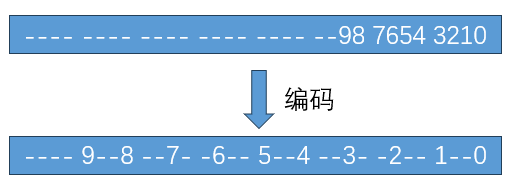
为了实现在比特位之间插入两个0的目标。最简单的实现就是使用循环语句去做,可是这样编码效率会降低。第二个是直接打表,把 0~1023 的结果编码预创建在数组里,然后直接索引,这样就是用空间换时间的做法,很快。第三个是利用位运算来操作,由于第三种方法引入了一个魔数,不太好理解,因此,在这里我想重点介绍第三种方法。
在公开的资料中,魔数背后的规律都没有仔细介绍。这里我就带着大家推导这几个魔数的由来,并解释为什么每次向左位移的距离是这些常数。
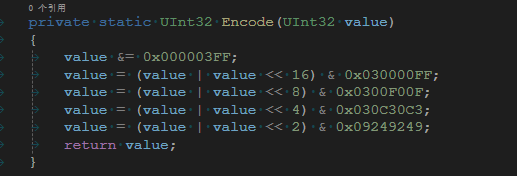
接下来就要讨论位移的长度和与魔数之间的关系。如果从原始输入从上往下推导,是不太好理解的,感觉就像是作者随意定的一组数字。然而如果从结果倒推,就可以找到数字背后的规律。
这里我们先来看魔数的作用。我们将数字左移,并和原来的数字进行合并。那么合并的结果,比特位数就是多余的,我们只需要把其中在需要保留的比特保留下来,把多余的剔除掉,这样就需要与一个常数,它可以把我们需要的比特保留,把不需要的去掉。
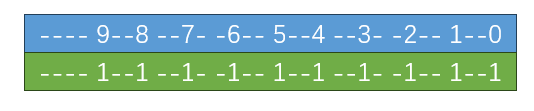
顺着这个思路,我们从结果倒推。可以看到编码结果中,10个比特位中间都插了两个0。

那么它上一次的输入,必然是与了下面绿色框里的数。它可以保留正确位置上的比特
它上一次的输入是一次左移两位的结果,左移的目的是为了把较高位的比特移动到正确的位置上,因此倒推出上一次输入结果如下:
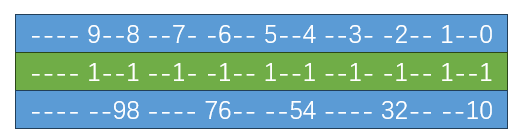
那么该结果的上一次输入,必然需要与一个数,如下
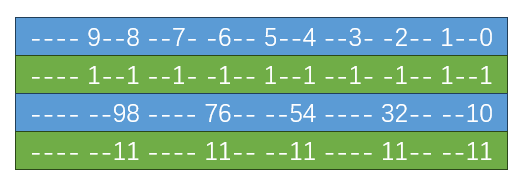
由此继续倒推,就可以推到原始的输入。

上图中绿色框内常数的推导,有一个规律,最上面的数字是一个显然的结果。然后逐层往下推,遵循一个法则:固定1个比特,在其左侧补1个1。

接着,以2个比特为固定比特,在左侧补2个1,如果比特数超过了10,就不需要补充

然后,以4个比特为固定比特,在左侧补4个1,如果比特数超过了10,就不需要补充。

最后,以8个比特位固定比特,在左侧补8个1,但不能超过10个比特。

综上可以得出,莫顿编码最高可以表示的坐标范围是[0,1023],1024就已经超出范围了。由上也可以知道,每次位移的数字是16,8,4,2的原由,它是为了固定最低位在正确的位置上,把高位分离出去,魔数的作用就是把分离出去之后,多余的bit给清除掉。由此可以总结出更高精度比特的规律。
单一整数解码
有了莫顿编码的过程,那么解码的过程也相当简单了。上面我们逆推导的过程,其实就是解码的过程。然后把上述过程倒过来写,就得到解码函数。
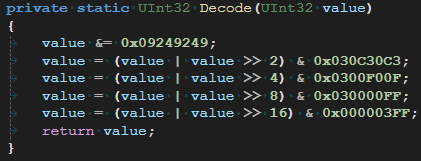
三维坐标编码
基于上面单一整数的编码过程。我们可以对三维坐标进行编码,然后我们会得到三个编码后的结果。对三个结果,我们要把它们合并到一起。合并操作如下

这样就得到了一个三维坐标的莫顿编码。合并顺序是Y,Z,X,这个是由个人喜好决定的。
三维坐标解码
在获得一个莫顿编码时。由于它把三个坐标的编码合到了一起,那么我们首先需要把单个坐标的编码解出来。这时候就需要编码时使用的魔数来提取了:

提取之后,得到单一整数的莫顿编码,就可以把执行单一整数的解码过程。得到原始坐标了
表示层数
有了三维坐标的莫顿编码结果。我们还需要表示该编码在稀疏八叉树中的层数。层数是从0开始计算的,第0层是叶子节点,最高层第10层是根节点。对于32位编码,还剩2个bit没用,所以可以拿它们来做文章,事实上,我们只需要一个bit即可。我们定义最右边比特的位置,作为编码的层数,即从第0位开始往左数的第1个1的位置。有了这个1比特的位置,就可以表示出树上的所有编码。如下图所示

层数增加时,这个比特需要左移到指定位置上,而坐标的莫顿编码也需要腾出空间来给这个比特,这样编码的比特空间利用率就获得了提高。
层数的编码
如上所述,层数和坐标会一起编码成一个UInt32整数。层数用最右侧1的位置来表示,1左侧是莫顿码。把所有结果整合在一起就是最终的编码。

层数的解码
根据上面的内容,我们知道莫顿编码和层数是如何表示的。那么解码的时候,就需要将层数和莫顿编码分开。根据上面的定义,要解开层数,需要知道最低位的第一个1所在的比特位置。通过下面的位运算,可以将最低位的1保留,而高位的所有数都置为0
private static UInt32 RightMostBit(UInt32 v)
{
return (v & (v - 1)) ^ v;
}
得到的结果,取指数即可得到Layer的结果。
public static int DecodeLayer(UInt32 code)
{
return (int)Math.Log(RightMostBit(code), 2);
}
有了Layer之后,将编码整体右移layer个bit,即可得到三维坐标的莫顿编码。如何根据上面的解码过程,就可以分别解出(X,Y,Z)三个坐标。至此,用32位整数表示一棵1024 x 1024 x 1024范围的稀疏八叉树的方案就此完成,其中每个节点的编码都代表一个体素坐标和节点所在层数(X,Y,Z,Layer)。
编码和体素包围盒的关系
Layer与体素节点大小关系是 size = 2^{Layer}。即第0层是叶子节点,表示大小为1的体素。逐层往上,表示的尺寸逐渐按2的次幂增长,到根节点为1024米。基于稀疏八叉树的数据结构开发的上层应用,经常需要将编码转换成AABB包围盒,AABB包围盒的表示就至关重要。包围盒的表示方式有两种:Center-Size和Min-Size,这里第二种表示方式时最适合这套编码系的。因为上面提到的坐标,就是AABB包围盒的Min。这样一来,体素包围盒的Min就编码成莫顿编码,体素包围盒的尺寸,就表示成Layer,这样整个稀疏八叉树的所有节点就可以完全表示了,而且内存占用不是特别高。
父子节点编码关系
编码之间的父子转换规律,与体素节点的坐标有关系,即上面10个比特表示的坐标。
在获得一个编码时,它的父节点坐标可以通过截断每一个维度坐标的最低位获得。

子节点坐标比较复杂,在计算第i个子节点坐标时,整数i的每一个bit对应到每一个维度的坐标最低位,即可计算出第i个子节点。假设三个bit分别表示下面的顺序。
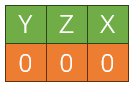
那么当对应位置的比特被设为1时,表示改子节点在该轴上为正向,当对应位置的比特为0时,则为另一个方向,即左右,上下,前后。这就是所谓的Z-Order了。
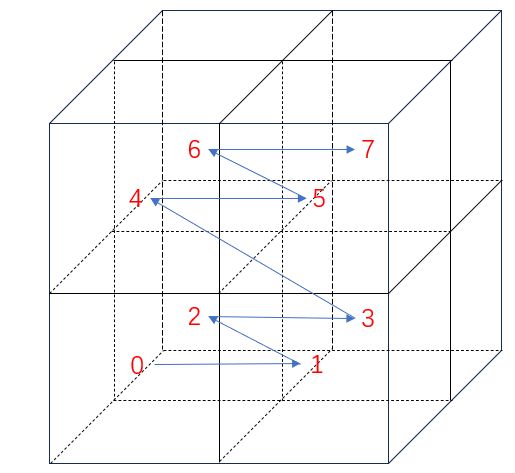
在计算子节点编码时,将坐标向左移,腾出1个比特的空间。然后根据整数 i 上对应轴的比特位,将该数字设置到坐标最低位上。然后layer减1,合起来就得到子节点编码。

编码数字背后的原理
用体素包围盒的Min来作为体素坐标时,我们会发现根节点的坐标,是(0,0,0)。而继续往下一层时,坐标都是0或1,即左右,上下,前后。而每次往更深层编码时,都是在进行左右,上下,前后的方向选择。每一次选择,都是一次二分的操作。
VTCode
综上所述的编码方法,Morton Code的魔数不太好理解。而且往每个比特中插入0的做法,是可以省去的。所以我提出如下改进:

可以直接将三个坐标合并到一起,然后和Layer-Bit组成编码。这样既方便理解,编码和解码都很快。且上述所有优势都没有丢失。
大范围场景的表示
上述编码只能表示1024 x 1024 x 1024的范围,当空间范围超过它时,编码就会溢出,为了表示更大范围的场景,就需要对场景进行均匀分块,每一块的范围是1024 x 1024 x 1024。这样的分块可以无限扩展,所以再大的范围都可以表示。只是在使用的时候,需要根据业务需求来对数据结构进行操作。
树空间和世界空间
上述的编码中,叶子节点是1米的单位距离。当需要表示更小的距离时,就需要进行缩放和转换。因此引入一个树空间,树空间最左下角点坐标是(0,0,0),对应到世界空间中的一个点。同时,树空间还定义了单位长度对应到世界空间中的长度,即缩放比例。这样使用上述编码表示的稀疏八叉树,在转换到世界空间时,叶子节点的尺寸就可以很灵活,只需要一个比例来控制。需要付出的相应的代价就是频繁的空间转换,在树上操作的结果,输出时要转换成世界空间,输入时要转换到树空间。实践中,这个开销时可以接受的。
嵌套的树结构
嵌套的树结构是我自己的猜想。如果一棵稀疏八叉树所定义的空间,与世界空间有一个转换比例。而在其中某个子空间,仍然想要获得更精细的比例时,就可以在这个空间中再嵌套一层树空间,使用另一个比例,这样的嵌套可以根据需求一直进行。这个操作应该理论上可行,不过没用进行实践验证。